
YAHWEH:
The Name Above All Names
The House of Yahweh – P.O. Box 2498 – Abilene, Texas 79604
A HOUSE OF YAHWEH®TM Publication COPYRIGHTED,© 2004 All Rights Reserved
When Yahweh gave His 613 Laws to Mosheh to teach to the Children of Israyl, He vowed an oath saying that those who would truly obey His voice and walk in all his ways would be a “special treasure”‘ to Him. He also promised that He would establish these Law-abiding people as his holy people.
Exodus 19:5-6—
5 Now therefore, if you will truly obey My voice, by keeping My covenant, then you shall be a special treasure to Me above all people; for all the earth is Mine.
6 And you shall be to Me a kingdom of priests, and a holy nation…Deuteronomy 28:9-10—
9 Yahweh will establish you as His Holy People unto Himself, as He promised you on oath, if you will keep the Laws of Yahweh your Father, and walk in all His ways.
10 Then all the people on the earth will see that you are called by the Name of Yahweh, and they will fear you.I Kepha 2:9—
But you are a chosen generation, a royal priesthood, a holy nation, a peculiar people; that you would show forth the praises of Him Who has called you out of darkness into His marvelous light.
These Scriptures show that all the people of the earth will see that Yahweh’s holy people (those who walk in all of Yahweh’s Ways) are known by the name of Yahweh. There has never been an inspired Scripture written in the Torah or by the prophets telling us that Yahweh’s holy people would ever be called (known) by any other name. In fact, the Prophet Yahyl was inspired to write a wonderful prophecy concerning everyone who calls with the name of Yahweh.
Yahyl 2:32—
And whoever will call with the Name of Yahweh will be delivered; for in Mount Zion in Yerusalem there will be deliverance, as Yahweh has said, among the remnant who has escaped of those whom Yahweh calls.Acts 2:21—
And it will come to pass that whoever calls on the Name of Yahweh will be delivered.Romans 10:13—
For Whoever calls with the Name of Yahweh will be saved.
Why is it that we do not call with the Name Yahweh? Do we not desire blessings? Do we not desire acceptance from our Father? Holiness? Salvation? Could it be that we’ve accepted traditions that our teachers have inherited from their teachers, and then taught to us as doctrine—doctrine that cannot be supported by the inspired Scriptures?
The Name Above All Names:
The Name Our Teachers Have Taught Us To Forget
We are not called by the Name of Yahweh, in fact Yahweh’s Name is not even uttered, because we have been taught that it is not acceptable to do so. We are taught that we must not pronounce the Holy Name of our Creator and Father, Yahweh, the Name the chosen of Yahweh will be known by, the Name those who are delivered will call upon! We are instructed by our teachers that Yahweh’s Name is too holy to pronounce; therefore, we are to call Him “Adonai” and “Elohim”.
This teaching has been fully ingrained in the minds of nearly all Israylites to the point that extreme hatred is shown toward anyone who openly speaks or writes the one and only true Name of the Creator. Remember this, because the holy prophets both spoke and wrote the true Name. As a result, the Name of Yahweh has almost been forgotten (in effect, profaned or brought to nothing), and Baal’s name is remembered and proclaimed worldwide.
A Name Remembered In Times Past But Unspoken Today
As we will read from authoritative sources, there was a time when the Name Yahweh was pronounced by all of Yahweh’s people, in prayers, in blessings, and in greetings. However, by the third century B.C.E., our teachers began teaching that Yahweh, the true Name of our Creator, was too holy to pronounce. This teaching is a practice that was not inspired by our Father, but one that gradually came about due to pagan influence.
At first, the practice was to just pronounce the name Adonai instead of the Name Yahweh, wherever Yahweh’s Name was written in the Holy Scriptures. However, as time went on, changes were made to the original writings. Vowel points (which were not originally part of the text) were added to Yahweh’s Name, causing the reader to pronounce the names Adonai and Elohim instead, and in many places these alternate names were actually written in place of Yahweh’s Name altogether. We’ll show you the many sources verifying these facts, but The Encyclopedia Judaica, Volume 7, pages 680-682, sums it all up rather well, as you can see for yourself.
YHWH. The personal name of the God of Israel is written in the Hebrew Bible with the four consonants yhwh and is referred to as the “Tetragrammaton”. At least until the destructions of the First Temple in 586 b.c.e., this name was regularly pronounced with its proper vowels, as is clear from the *Lachish Letters, written shortly before that date. But at least by the third century b.c.e., the pronunciation of the name yhwh was avoided, and Adonai, “the Lord”, was substituted for it, as evidenced by the use of the Greek word Kyrios, “Lord”, for yhwh in the Septuagint, the translation of the Hebrew Scriptures that was begun by Greek-speaking Jews in that century. Where the combined form *Adonai yhwh occurs in the Bible, this was read as *Adonai *Elohim, “Lord God“. In the early Middle Ages, when the consonantal text of the Bible was supplied with vowels points to facilitate its correct traditional reading, the vowel points for ‘Adonai with one variation – a sheva with the first yod of YHWH instead of the hataf-patah under the aleph of ‘Adona’ were used for YHWH, thus producing the form Yehowah. When Christian scholars of Europe first began to study Hebrew, they did not understand what this really meant, and they introduced the hybrid name “Jehovah”. In order to avoid pronouncing even the sacred name *Adonai for YHWH, the custom was later introduced of saying simply in Hebrew ha-Shem (or Aramaic Shemc, “the Name”) even in such an expression as “Blessed be he that cometh in the name of YHWH” (Ps. 118:26).
THE PROHIBITION OF USE OF THE NAMES OF GOD. The prohibition applies both to the pronunciation of the name of God and its committal to writing, apart from its use in sacred writings. The prohibition against the pronunciation of the name of God applies only to the Tetragrammaton, which could be pronounced by the high priest only once a year on the Day of Atonement in the Holy of Holies (cf. Mishnah Yoma 6:2), and in the Temple by the priests when they recited the Priestly Blessings (Sot. 7:6; see also Ch. Albeck (ed.), Seder Nashim (1954), 387). As the Talmud expresses it: “Not as I am written am I pronounced. I am written yod he vav he, and I am pronounced alef dalet” (nun yod, i.e., Adonai; Kid. 71a).
The Prohibition Of Yahweh’s Name
Authoritative scholars, such as the one shown above, point out that the original, personal name of our Creator, written 
In ancient times, the Hebrew words were written without vowels in what is called the unpointed script, so that each word consisted of a group of consonants whose vowel sounds were supplied from memory by the reader. In other words, Hebrew words were pronounced with vowel sounds even though the vowels themselves were not written. The Hebrews knew, from oral teaching and practice, which vowels were associated with the different words. Yahweh’s Name is written yod-heh-waw-heh 
It thus becomes possible to determine with a fair degree of certainty the historical pronunciation of the Tetragrammaton, the results agreeing with the statement of Ex. iii. 14, in which YHWH terms Himself
. “I will be”, a phrase which is immediately proceeded by the fuller term “I will be that I will be,” or, as in the English versions, “I am” and “I am that I am.” The name
is accordingly derived from the root
(=
), and is regarded as an imperfect. This passage is decisive for the pronunciation “Yahweh”; for the etymology was undoubtedly based on the known word.
The Encyclopedia Judaica, Volume 7, page 680, further states this fact.
The true pronunciation of the name YHWH was never lost. Several early Greek writers of the Christian Church testify that the name was pronounced “Yahweh“. This is confirmed, at least for the vowel of the first syllable of the name, by the shorter form Yah, which is sometimes used in poetry (e.g., Ex. 15:2) and the -yahu or -yah that serves as the final syllable in very many Hebrew names.The Encyclopedia Britanica, Volume 23, page 867, confirms this fact.
YAHWEH, the proper name of the God of Israel; it is composed of four consonants (YHWH) in Hebrew and is therefore called the Tetragrammaton…The Universal Jewish Encyclopedia, Volume 9, page 160, confirms this fact.
Of the names of God in the Old Testament, that which occurs most frequently (6,823 times) is the so-called Tetragrammaton, YHWH (), the distinctive personal name of the God of Israel.
And The Jewish Encyclopedia Volume 12, pages 118-119, confirms this fact also.
TETRAGRAMMATON: The quadriliteral name of God, (). The Tetragrammaton is the ancient Israelitish name for God…
The Jewish Encyclopedia, Volume 9, pages 162-163, also shows us that while the rabbis recognized only one proper name for the Creator, they also considered other names as titles for the Creator. As you read this excerpt, notice and remember the title (Adonai) that was used in place of the Creator’s Name:
…The Rabbis as well as the cabalists steadfastly maintained their belief in monotheism. Hence they recognized only one proper name for the Deity, considering the other names as appellations or titles signifying divinity, perfection, and power, or as characterizing His acts as observed and appreciated by mankind…The name YHWH is considered as the Name proper; it was known in the earliest rabbinical works simply as the Name; also as Shem ha-Meyuhad (“the Extraordinary Name”; Sifre, Num. 143): as Shem ha-Meforash (“the Distinguished Name”; Yoma vi. 2); as Shem ben The Name. Arba’ Otiyyot (“the Tetra-grammaton” or “the Quadrilateral Name”; Kid 71a); and as Yod He Waw He (spelling letters of YHWH).
It is recorded that the pronunciation of the Name Yahweh began to be suppressed in earnest upon the death of a man named Simeon the Just, a High Priest who served in this office in the time span of 310-199 B.C.E., or about 200 years before the nation of Israyl came under the rulership of the Roman Empire. The Jewish Encyclopedia of 1901, Volume 11, page 353, points out that this was the turning point, namely the exact time when it became a practice in Israyl to no longer pronounce the Name Yahweh.
SIMEON THE JUST (
): High priest. He is identical either with Simeon I. (310-291 or 300-271 b.c.), son of Onias I., and grandson of Jaddua, or with Simeon II. (219-199 b.c.), son of Onias II… After Simeon’s death men ceased to utter the tetragrammaton aloud (Yoma 30b; Tosef Sotah. xiii.).
The Babylonian Talmud, Tractate Yoma, page 39b, also verifies that it was upon the death of Simeon the Righteous, that all Israyl began to no longer pronounce the Name Yahweh.
…When Simeon the Righteous died, with many indications that such glory was no more enjoyed, his brethren no more dared utter the Ineffable Name…
The Jewish Encyclopedia Volume 9, pages 162-163, not only confirms this fact, but it shows the strict prohibition and warning to all those who do not adhere to it.
The restriction upon communicating the Name proper probably originated in Oriental etiquette; in the East even a teacher was not called by name. For naming his master Elisha, Gehazi was punished with leprosy (II Kings viii. 5; Sanh. 100a). After the death of the high priest Simeon the Righteous, forty years prior to the destruction of the Temple, the priests ceased to pronounce the Name (Yoma 39b). From that time the pronunciation of the Name was prohibited. “Whoever pronounces the Name forfeits his portion in the future world” (Sanh. xi. 1). Hananiah ben Teradion was punished for teaching his disciples the pronunciation of the Name (`Ab. Zarah 17b).
The Babylonian Talmud, Tractate Kiddushin, page 71a, openly admits, however, that the Name Yahweh was pronounced by all the children of Israyl, both small and great, before the death of Simeon the Just.
Our Rabbis taught: At first [Yahweh’s] Name used to be entrusted to all people. When unruly men increased, it was confided to the pious of the priesthood
Only The High Priest Spoke The Name Of Yahweh
Many teachers in Israyl came to believe that the Name Yahweh was too holy to be pronounced, so they began teaching the nation that only the High Priest should utter this Name, once a year on the Day of Atonement. The Century Bible, by Adeney and Bennett, Volume 1, pages 90-91, shows us this information.
Some time after the return from the Captivity, and before the beginning of the Christian era, the Jews came to believe that the Name YHWH was too sacred to be uttered on ordinary occasions. It was said to be pronounced by the High Priest on the Day of Atonement.
Please note the time period in which the Name of our Heavenly Father was suppressed, some time after the return from the captivity, and before the beginning of the Christian Era (approximately 310-199 B.C.E.). This means that up to this time, the prophets, and in fact all the people of Israyl, used the great Name of Yahweh when they walked through the waters of the Red Sea; when they ate manna which came directly from Yahweh; when they saw their enemies expelled from in front of them; when they took the lands from their enemies; and all the while, they were becoming a healthy nation. It was only in turning from Yahweh to idolatry, as we are doing today, that caused Yahweh to hide His face from Israyl and give their enemies advantage over them.
The Jewish Encyclopedia contains additional information about the pronunciation of Yahweh’s Name being confined to the temple and spoken only by the priests. Volume 9, pages 162-163, states: The pronunciation of the written Name was used only by the priests (Num. vi. 22-27); outside the Temple they used the title “Adonai” (Sotah vii. 6; p. 38a)…
Volume 1, pages 201-202, shows us this:
…In the early period of the Second Temple the Name was still in common use, as may be learned from such proper names as Jehohanan, or from liturgical formulas, such as Halelu-Yah. At the beginning of the Hellenistic era, however, the use of the Name was reserved for the Temple. From Sifre to Num. vi. 27, Mishnah Tamid, vii. 2, and Sotah, vii. 6 it appears that the priests were allowed to pronounce the Name at the benediction only in the Temple; elsewhere they were obligated to use the appellative name (kinnuy) “Adonai”‘ …
…Pronunciation of the Name by the Temple priests… also gradually fell into disuse. Tosef., Sotah, xiii. 8 quoted Menahot, 109b, and Yoma 39b, relates that “from the time Simon the Just died [this is the traditional expression for the beginning of the Hellenistic period], the priests refrained from blessing the people with the Name“__in other words, they pronounced it indistinctly, or they mouthed or mumbled it. Thus says Tosef., Ber. vi. 23: Formerly they used to greet each other with the Ineffable Name; when the time of the decline of the study of the Law came, the elders mumbled the Name. Subsequently also the solemn utterance of the Name by the high priest on the Day of Atonement, that ought to have been heard by the priests and the people according to the Mishnah Yoma, vi. 2, became inaudible or indistinct.
R. Tarfon (or Tryphon) relates (Yer. Yoma, iii. 40d): “I was standing in the row of young priests, and I heard the high priest mumbling the Name, while the rest of the priests were chanting.”
…But while even among these the right pronunciation was forgotten in the course of time, and the hope was expressed by Phinehas b. Jair, “the Saint”, that the knowledge and the correct use of the Name, so wondrously efficacious in the blessed days long goneby, would again be restored in the Messianic age (see Pes. 50a, Midr. Teh. to Ps. xxxvi. and to Ps. xci.)…
Volume 11, page 263, shows us more:
…the Mishnah (Sotah vii. 6; Tamid vii. 2) says, in conformity with this interpretation: “In the Sanctuary the name of God [in the three blessings, Num. vi. 24-26] is to be pronounced in the Priestly Benediction as it is written [

The Shem ha-Meforash as an object of the esoteric knowledge of scholars appears in the statement of Johanan (Kid. 71a): “Once each week the sages give their pupils the Four-Lettered Name.” A tannaitic passage in Yer. Yoma 40d, however, says: “In former times the Name was taught to all; but when immorality increased it was reserved for the pious,” although this statement refers, according to the baraita in Kid. 71a, to teaching the Name to the priests.
The Name of Yahweh Engraved on an Ivory Pomegranate Decoration

Immorality came among the people because Yahweh and His Laws were not being taught or practiced. So without authority from the inspired words of the prophets, our forefathers removed the name of Yahweh from the memory of our people. Instead of teaching Yahweh’s Laws, they turned to the traditions of the Gods of earth and heaven!
Process Of Elimination Developed And Implemented
In order to implement the avoidance of pronouncing Yahweh’s Name (
The Jewish Encyclopedia, Volume 12, pages 118-119, tells us more about this:
TETRAGRAMMATON: The quadrilateral name of God, (
The Tetragrammaton is the ancient Israelitish name for God. According to actual count, it occurs 5,410 times in the Bible, being divided among the books as follows: Genesis 153 times, Exodus 364, Leviticus 285, Numbers 387, Deuteronomy 230, (total in Torah 1,419); Joshua 170, Judges 158, Samuel 423, Kings 467, Isaiah 367, Jeremiah 555, Ezekiel 211, Minor Prophets 345 (total in Prophets 2,696); Psalms 645, Proverbs 87, Job 31, Ruth 16, Lamentations 32, Daniel 7, Ezra__Nehemiah 31, Chronicles 446 (total in Hagiographa 1,295).
In connections with (

The Interpreters Dictionary of the Bible, Supplementary Volume, page 717, tells us more about the devices used to hide Yahweh’s Name:
Qere perpetuum. The earliest instance where a word in the biblical text was not read, but another was pronounced in its stead, is that of the TETRAGRAMMATON (YHWH). The prohibition of pronouncing “The Name,” and the obligation of substituting in perpetuity a term that expresses the divine majesty, are explicitly recognized in the Babylonian Talmud (Pes. 50a): “Said the Holy One, blessed be He: not as I am written, am I read. I am written
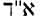
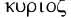


This ancient prohibition of pronouncing the divine name persisted orally until the introduction of the Hebrew vocalic system, where the vowels written under the Tetragrammaton are those of the substitute word Adonai. Its antiquity clearly shows that it originated in the oldest Jewish oral traditions that accompanied the transmission (masora) of the sacred text from the beginning. In contrast to the qere perpetuum, substituted orally for the Tetragrammaton, the Masoretic tradition, as a precautionary measure, indicated in the margin of later mss, in the form of a statistical note (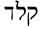

Robert Pfeiffer, in his Introduction to the Old Testament, supplies more information:
To avoid the utterance of the name Yahweh, both before and after the adoption of the qere, other devices were employed. In some cases adonay was written in the text (so in Dan. 9:9 where the Babylonians wrote YHWH); in Pss. 42-83 elohim (deity) is substituted for Yahweh; in Am. 5:16 adonay (missing in the lxx) and in Ps. 59:5 (H. 59:6); 80:4, 19 (H. 80:5, 20); 84:8 (H. 84:9) elohim are interlinear substitutes for yhwh, which were mechanically copied into the text (see W.R. Arnold, Ephod and Ark, pp. 31, 38, 145-147). We even find in the text late substitutes for Yahweh: “Heaven” (Dan. 4:26 [H. 4:23]; cf. Is. 14:13, lxx; the Kingdom of “Heaven” in Matthew) and “the Name” (Lev. 24:11, 16). In the Aramaic portions of Daniel 2-7, not only are substitutes for Yahweh regularly employed, but the verbal form YeHeWeH (he is or will be), which occurs regularly in the Elephantine papyri, to avoid confusion with the ineffable name YHWH was changed to LeHeWeH (similarly the plurals lehewon, lehewyah).
Long after the introduction of the qere “Lord” for YHWH (6,823 times in the Old Testament according to the Masora), but before a.d. 500, vulgar expressions in the text, as we have seen, were removed by substituting a euphemism in the reading (qere). Equally ancient are the instances of “read but not written” and “written but not read” listed above.
Vowel points were placed among the letters of Yahweh’s Name 

Hebrew was originally written without vowels, but when the vowel points were added, the vowels of Adonay or Elohim were written with yhwh, as a direction that these words were to be read instead of the word whose consonants were YHWH. Thus we find the combinations YeHoWaH and YeHoWiH.
We have already seen that the two names chosen to take the place of the Name Yahweh are Adonai and Elohim. When the vowel points of Adonai or Elohim were placed among the letters of the Name Yahweh 
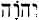
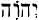
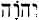
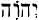
…R. Abina opposed [two verses]: It is written, ‘this is my name’; but it is also written, ‘and this is my memorial’?__The Holy One, blessed be He, said: I am not called as I am written: I am written with yod he, but I am read, alef daleth.7
7. The Tetragrammaton is yod he waw he; but it is read adonai = alef daleth nun yod…
Our Father’s Name: Lost Through Translations
To Other Languages
We have plainly seen that due to the devices of our teachers and leaders, the rabbis, the Name of Yahweh fell into disuse. What started out in speech, also was transferred into writing. The Name of Yahweh was replaced with the name Adonai so that down through the years, especially in the translation from Hebrew to other languages, The Holy Scriptures do not contain the Name of yahweh at all, but rather the title Lord.
The Encyclopedia Britanica, Volume 23, page 867, confirms the fact that the proper, original Name Yahweh was replaced with common substitutes:
YAHWEH, the proper name of the God of Israel; it is composed of four consonants (YHWH) in Hebrew and is therefore called the tetragrammaton…
The name Yahweh later ceased to be used by the Jews for two somewhat contradictory reasons. As Judaism began to become a universal religion, the proper name Yahweh tended to be replaced by the common noun Elohim, meaning “God,” which could apply to foreign deities and therefore could be used to demonstrate the universal sovereignty of Israel’s God over all others. At the same time, the divine name was increasingly regarded as too sacred to be uttered, for fear of profanation, and in the synagogue ritual it was replaced by Adonai (“my Lord”), which was translated Kyrios (“Lord”) in the Septuagint. The occurence of the four sacred letters in the text of the Bible itself could not be thus replaced, but the same fear of profanation caused Masoretes (6th-8th centuries a.d.) to change the pronunciation by replacing the vowels (which in Hebrew are marked beneath or above the consonants if not omitted altogether) with the vowels of Adonai (or, more rarely, the vowels of Elohim).
The Jewish Encyclopedia, Volume 1, pages 201, 203, also points out this fact.
ADONAI (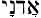
…No wonder, then, that the Greek translators of the Bible, even though some scribe might now and then write the Tetragrammaton in the archaic Hebrew form on the margin, II I II I, as found by Origen (see facsimile attached to article AQUILA), took great care to render the name II I II I regularly Kupios, Lord, as if they knew of no other reading but Adonai. Translations dependant upon the Septuagint have the same reading of the Name.
You have just read proof after proof that the words Adonai and Elohim have come to be substituted for the Name Yahweh, whether in speech or in writing, throughout The Holy Scriptures so that Yahweh’s Name is forgotten. However, the simple fact remains, in the very earliest writings, known as the J or Yahwist manuscripts, the Name of Yahweh is used exclusively. So then, how did these words come to be accepted as suitable substitutes for the Name Yahweh?
Fragments from the Septuagint showing YAHWEH’s Name
(The Septuagint is written in Greek, but YAHWEH’s Name is written in the ancient Hebrew)
Process Of Elimination Developed And Implemented
In order to implement the avoidance of pronouncing Yahweh’s Name (
The Jewish Encyclopedia, Volume 12, pages 118-119, tells us more about this:
TETRAGRAMMATON: The quadrilateral name of God, (
The Tetragrammaton is the ancient Israelitish name for God. According to actual count, it occurs 5,410 times in the Bible, being divided among the books as follows: Genesis 153 times, Exodus 364, Leviticus 285, Numbers 387, Deuteronomy 230, (total in Torah 1,419); Joshua 170, Judges 158, Samuel 423, Kings 467, Isaiah 367, Jeremiah 555, Ezekiel 211, Minor Prophets 345 (total in Prophets 2,696); Psalms 645, Proverbs 87, Job 31, Ruth 16, Lamentations 32, Daniel 7, Ezra__Nehemiah 31, Chronicles 446 (total in Hagiographa 1,295).
In connections with (

The Interpreters Dictionary of the Bible, Supplementary Volume, page 717, tells us more about the devices used to hide Yahweh’s Name:
Qere perpetuum. The earliest instance where a word in the biblical text was not read, but another was pronounced in its stead, is that of the TETRAGRAMMATON (YHWH). The prohibition of pronouncing “The Name,” and the obligation of substituting in perpetuity a term that expresses the divine majesty, are explicitly recognized in the Babylonian Talmud (Pes. 50a): “Said the Holy One, blessed be He: not as I am written, am I read. I am written
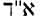
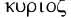


This ancient prohibition of pronouncing the divine name persisted orally until the introduction of the Hebrew vocalic system, where the vowels written under the Tetragrammaton are those of the substitute word Adonai. Its antiquity clearly shows that it originated in the oldest Jewish oral traditions that accompanied the transmission (masora) of the sacred text from the beginning. In contrast to the qere perpetuum, substituted orally for the Tetragrammaton, the Masoretic tradition, as a precautionary measure, indicated in the margin of later mss, in the form of a statistical note (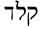

Robert Pfeiffer, in his Introduction to the Old Testament, supplies more information:
To avoid the utterance of the name Yahweh, both before and after the adoption of the qere, other devices were employed. In some cases adonay was written in the text (so in Dan. 9:9 where the Babylonians wrote YHWH); in Pss. 42-83 elohim (deity) is substituted for Yahweh; in Am. 5:16 adonay (missing in the lxx) and in Ps. 59:5 (H. 59:6); 80:4, 19 (H. 80:5, 20); 84:8 (H. 84:9) elohim are interlinear substitutes for yhwh, which were mechanically copied into the text (see W.R. Arnold, Ephod and Ark, pp. 31, 38, 145-147). We even find in the text late substitutes for Yahweh: “Heaven” (Dan. 4:26 [H. 4:23]; cf. Is. 14:13, lxx; the Kingdom of “Heaven” in Matthew) and “the Name” (Lev. 24:11, 16). In the Aramaic portions of Daniel 2-7, not only are substitutes for Yahweh regularly employed, but the verbal form YeHeWeH (he is or will be), which occurs regularly in the Elephantine papyri, to avoid confusion with the ineffable name YHWH was changed to LeHeWeH (similarly the plurals lehewon, lehewyah).
Long after the introduction of the qere “Lord” for YHWH (6,823 times in the Old Testament according to the Masora), but before a.d. 500, vulgar expressions in the text, as we have seen, were removed by substituting a euphemism in the reading (qere). Equally ancient are the instances of “read but not written” and “written but not read” listed above.
Vowel points were placed among the letters of Yahweh’s Name 

Hebrew was originally written without vowels, but when the vowel points were added, the vowels of Adonay or Elohim were written with yhwh, as a direction that these words were to be read instead of the word whose consonants were YHWH. Thus we find the combinations YeHoWaH and YeHoWiH.
We have already seen that the two names chosen to take the place of the Name Yahweh are Adonai and Elohim. When the vowel points of Adonai or Elohim were placed among the letters of the Name Yahweh 
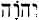
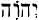
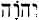
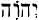
…R. Abina opposed [two verses]: It is written, ‘this is my name’; but it is also written, ‘and this is my memorial’?__The Holy One, blessed be He, said: I am not called as I am written: I am written with yod he, but I am read, alef daleth.7
7. The Tetragrammaton is yod he waw he; but it is read adonai = alef daleth nun yod…


The following is a photo of Psalms 119:59-64 in the Dead Sea Scrolls which are a collection of Hebrew Scriptures that date back 2000 years. Note Yahweh’s name in the ancient Hebrew script while the rest of the text is in a more modern Hebrew that was used at the time.
The Four Main Manuscripts
The general consensus among scholars is that there are four main sources or manuscripts of The Holy Scriptures named J, E, P, and D. The Encyclopedia Judaica, Volume 13, page 234, gives us this fact.
Sources. The opinion accepted in contemporary biblical research is that the pentateuchal literature is composed of four major sources: J, E, P, and D.
This information concerning the major sources of the Scriptures is also shown to us in The Encyclopedia Brittanica, Volume 2, page 194:
BIBLICAL SOURCE, any of the original documents that, in compilation, constitute the Bible. Most of the writings in the Old Testament are of anonymous authorship, and in many cases it is not known whether they were compiled by individuals or by groups. Nevertheless, by careful evaluation of internal evidence and with the aid of various schools of biblical criticism (q.v.), scholars have been able to identify certain sources and to arrange them chronologically in order of composition.
The means by which the basic sources of the Pentateuch (first five books of the Bible) were distinguished and their chronology established provided the first clear picture of Israel’s literary and religious development. The names by which these sources are now known, in chronological order, are: the Yahwist, or J, source, so called because it employed as the Lord’s name a Hebrew word transliterated into English as YHWH (called J from the German: JHVH) and spoken as Yahweh; the Elohist, or E, source, distinguished by its reference to the Lord as Elohim; the Deuteronomist, or D, source, marked by distinctive vocabulary and style; and the Priestly code, or P, source, which contains detailed ritual instructions.
Our main concern will focus on the J and E sources. It is very important to note that the oldest source, the J exclusively. Yes, in the oldest manuscript of the Scriptures, Yahweh is never referred to by the titles El, Elohim, or Adonai—but only by His Name, Yahweh! (Yahwist) source, used the Name of Yahweh
The Encyclopedia Judaica, Volume 13, page 234, gives us these facts:
…The distinction between J and E is based primarily on the different usage of the divine name in these sources: YHWH in J and Elohim (“God”) in E. P is the Priestly Source and D the Deuteronomic. The different usage of the divine name is not only a matter of form but relates to the type of attitude taken to the history of the religion of Israel. According to J, YHWH, the Lord of Israel, was worshipped as early as the time of Enosh (Gen. 4:26), while according to E, YHWH, i.e., the true name of the God of Israel, was first revealed to Moses at the burning bush (Ex. 3:6ff.).
…J notes a religious continuity beginning with the time of Enosh and continuing through the period of the Patriarchs to Moses. In contrast, E and P, while admitting that the God who was revealed to the Patriarchs is the God who was revealed to Moses, maintain that the Patriarchs did not know Him by His true name, and there is doubtless theological significances to this lack of knowledge. Furthermore, P, which places great emphasis on the religious chasm between the period of the Patriarchs and that of Moses, does not consider the possibility of legitimate worship of God (sacrifices) before the revelation in the time of Moses.
J and E Sources. This difference between J and E is most evident in Genesis, where it is based on an explicit criterion: YHWH in J as opposed to Elohim in E…
The J (Yahwist) Source
The Jewish Encyclopedia, Volume 7, pages 64-65, tells us also that the J manuscript preferred the Name of Yahweh over Elohim:
…(usually symbolized as J): The name given in modern Bible criticism to the supposed author of those portions of the Pentateuch (or of the Hexateuch) in which the name yhwh is used for God in preference to the name “Elohim,” which latter is employed by the Elohistic writers.
..it is natural to suppose that J was written as its counterpart, and as an expression of the view that YHWH ruled all things from the beginning, and that the faith and worship cherished in Jerusalem were also those of the Fathers.
The Interpreter’s Dictionary of the Bible, Volume 2, page 777, tells us this about the oldest source of The Holy Scriptures, the Yahwist source:
J. One of principal narrative sources or strata of the Pentateuch. The symbol is derived from the personal name of God, Jehovah (or more accurately Yahweh, from 
The Anchor Bible, Genesis, Volume 1, pages 37-38, confirms that the J source is the oldest (and therefore the first and inspired) source of the Scriptures:
…J traced back the name Yahweh to the dim past, while E and P attributed the usage to Moses, both views may be justified depending on the point vantage. The worship of Yahweh was in all likelihood confined at first to a small body of searchers under the aegis of the patriarchs; it was this movement that found a worthy recorder in J. When Moses set out to fashion a nation out of an amorphous conglomerate of sundry ethnic and tribal elements, he had to concentrate on three major features of nationhood: a territorial base, a body of laws, and a distinctive religion. The last was normative in more ways than one; it was necessarily the faith of the same forefathers who had already tied it to the Promised Land, with Yahweh as its fountainhead. To that extent, therefore, Yahweh revealed himself to Moses: and it is this personal revelation that both E and P celebrate. To J, however, who chronicled the progress within the inner circle of the patriarchal pioneers, the personal participation of Yahweh had been the dominant fact from the start.
The Encyclopedia Judaica, Volume 7, pages 680-681, concerning this “J” writer, says:
According to the documentary hypothesis, the literary sources in the Pentateuch known as the Elohist and the Priestly Document never use the name Yahweh for God until it is revealed to Moses (Ex. 3:13; 6:2-3); but the Yahwist source uses it from Genesis 2:4 on, thus implying that it was at least as old as Abraham. If the name is really so old, then Exodus 6:2-3 must be understood as meaning that from the time of Moses on, Yahweh was to be the personal name of the God who brought the people of Israel into existence by bringing them out of Egypt and established them as a nation by His covenant with them at Sinai.
One must wonder, if Abraham and Mosheh had followed the same teaching we today have known from birth, the Name of our Heavenly Father would have never been known to us today. It is my opinion that we should praise Yahweh for giving Abraham and Mosheh the great wisdom to call upon, and write for us, His Name.
The Interpreters Dictionary of the Bible, Volume 2, page 409, confirms the fact that the earliest manuscripts used only the Name Yahweh.
...The Yahwist narrative (see Pentateuch) traces the worship of Yahweh far back beyond the period of Moses and affirms that in the time of Enosh, the grandson of Adam, men first began to invoke the name of Yahweh (Gen. 4:26). This narrator’s consistent use of the name from the story of Creation onward represents a theological attempt to view the whole of human history in the light of the covenant faith and to demonstrate that Yahweh is not just the God of Israel but of all mankind (Enosh means “man”)…
…Although the name was given new currency in Mosaic circles, the J account (Gen. 4:26) may preserve a dim recollection that it was known in the pre-Mosaic period….
…However, the latest Pentateuchal tradition, the priestly writing (P), gives a completely different view in Exod. This conjecture is confirmed by a third Pentateuchal tradition, E, which avoids using Yahweh in the book of Genesis…
…In the earliest Hebrew the sacred name appeared as a four-letter word or tetragrammaton: YHWH –
Knowing the time in which the blinded scribes began to replace Yahweh’s Name with titles of gods and Lords, and then reading the rebuke given to them by the Prophet Yeremyah (Chapter 23) for making Yahweh’s people forget His great Name, we see the pieces of an historical puzzle start falling into place. After rejecting and hiding Yahweh’s Name, it’s obvious that the next step was to reject and deny Yahweh’s great laws.
The translation of the Holy Scriptures from Hebrew to Aramaic, the Targums, are known for their literal adherence to the original Hebrew Scriptures which used the Name Yahweh. The Chumash with Targum Onkelos and Rashi’s Commentary, shows us that in Genesis 1:1, where Elohim is used in the Masoretic text, the Targum Onkelos uses the Aramaic abbreviation for Yahweh.
Masoretic Text: The word ELOHIM is circled
Targum Onkelos: The Name YAHWEH is circled
The E (Elohist) Source
The E or Elohist source is derived from the word elohim, god, the use of which is characteristic of this source. Please remember, the J (Yahwist) source is the oldest source, meaning the Elohist source came after the Yahwist source. The Interpreters Dictionary of the Bible, Volume 2, page 1, tells us:
E (ELOHIST) -. One of the principal narrative sources or strata of the Pentateuch. The term is derived from a Hebrew word for “God” (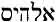
The Jewish Encyclopedia, Volume 5, page 142, confirms that the E source used Elohim in place of Yahweh’s Name.
…The use of “Elohim” for “God” is the most notable characteristic of E. …the symbol J (=Jahvist) applying to passages in which the name “YHWH” is predominant. “Adonai” and “El” occur occasionally (Gen. xx. 4, xxx. 20, xxxv. 7, xliii. 14).
The Interpreter’s Dictionary, Volume 2, page 94, also shows that this source is commonly associated with the Northern Kingdom of Israyl, and dates approximately 100 years later than the Yahwist source.
ELOHIST, The author or compiler of the E source of the Pentateuch (see E), which is commonly associated with the N kingdom and dated to the eighth century b.c.
The Anchor Bible, Proverbs-Ecclesiastes, Volume 18, page xxxi, tells us that the Elohist (E) source shows its ORIGIN to be in the NORTHERN KINGDOM of Israyl, when the kingdom split in two AFTER the death of Solomon:
The fact that the E document in the Pentateuch shows evidences of origin in North Israel after the division of the kingdom at Solomon’s death, but follows the outline of the Judean J document which it later was used to supplement, indicates that both stem from a common source before the kingdom split in two.
Do you grasp the significance of this? This says that both the Yahwist and the Elohist sources stem from a common source before the kingdom split in two. This actually means they used the same work, however, while one retained Yahweh’s Name in the Holy Scriptures, the other replaced Yahweh’s Name with the title Elohim.
The Universal Jewish Encyclopedia, Volume 9, page 160, gives us more proof that Yahweh’s Name appeared in the original writings, and Adonai and Elohim were added later.
Of the names of God in the Old Testament, that which occurs most frequently (6,823 times) is the so-called Tetragrammaton, YHWH (

This name, according to the narrative in Ex. iii. (E), was made known to Moses in a vision at Horeb. In another, parallel narrative (Ex. vi. 2, 3, P) it is stated that the name was not known to the Patriarchs. It is used by one of the documentary sources of Genesis (J), but scarcely if at all by the others. Its use is avoided by some later writers also. It does not occur in Ecclesiastes, and in Daniel is found only in ch. ix. The writer of Chronicles shows a preference for the form Elohim, and in Ps. xliii.-lxxxiii. Elohim occurs much more frequently than YHWH, probably having been substitued in some places for the latter name , as in Ps. liii. (comp. Ps. xiv.).
The Ancient And Honored Name Of Yahweh


It was three years after its discovery before this fragile amulet could be unrolled by technical experts at the Israyli Museum. On this amulet the Name of Yahweh could be clearly read. Complete details of this magnificent find can be read in the 6-28-86 and 8-9-86 issues of The Jerusalem Post and the 6-87 issue of The Readers Digest.
The following excerpt was taken from an article in the November/December 1997 issue of Biblical Archaeology Review, pages 28-32. We see here that the Creator’s work during the time of Solomon was known by the same Name as it is today—The House of Yahweh. It was Solomon who built the Temple where this tithe was given. You can read of this in I Kings 6.
Three Shekels For The Lord
Ancient Inscription Records Gift To Solomon’s Temple
Two extremely important Hebrew inscriptions have recently surfaced on the antiquities market. One appears to be a receipt for a donation of three silver shekels to the House of Yahweh, pursuant to an order of the Israelite king. This is the oldest extra-Biblical mention of King Solomon’s Temple ever discovered. The other inscription records the petition of a widow for some portion of her late husband’s property. Both inscriptions, apparently by the same scribe, are written in Old Hebrew, or paleo-Hebrew, the script used before the Babylonian Exile. Both are on pieces of pottery, called ostraca because they bear an inscription.
Only one other extra-Biblical source mentions Solomon’s Temple, destroyed by the Babylonians in 586 B.C.E…
The text on the first ostracon, which measures about 4 inches wide by 3.5 inches tall (10.9 by 8.6 cm), is only 5 lines and 13 words long. All the words are complete and readable. See the box for the text and translation.
A TEMPLE RECEIPT
Text:
1. K’SR SWK. ‘SY
2. HW.HMLK.LTT.BYD
3. [Z]KRYHW.KSP TR
4. SS.LBYT YHWH [.]
5. S3
Translation:
1. Pursuant to the order to you of Ashya-
2. hu the king to give by the hand
3. of [Z]echaryahu silver of Tar-
4. shish to the House of Yahweh
5. Three shekels.
*Brackets indicate that the letter or word has been reconstructed. Half-brackets indicate that part of the leter or word has been reconstructed.
Most of the words are separated from one another by dots acting as word dividers. However, sometimes the word dividers are omitted, such as between LBYT and YHWH, which together are pronounced Beit Yahweh and mean “House of Yahweh.”
The Temple is designated by the Hebrew term BYT YHWH, many times in the Bible. (Temple only refers to the building, Beit—House refers also the people of Yahweh). But BYT YHWH had been found complete in only one extra-Biblical inscription, a faded ostracon from Arad with an obscure context, until this newly published ostracon was revealed.
BYT YHWH has been reconstructed on the inscribed ivory pomegranate that served as the head of a priestly scepter in Solomon’s Temple… divine name would mean “he causes to be, or exist,” i.e., “he creates.” Amorite personal names after 2,000 B.C. lend support to the Haupt-Albright view, demonstrating that the employment of the causative stem yahwe “he creates” was in vogue in the linguistic background of early Hebrew.
The Interpreter’s Dictionary of the Bible, Volume 4 page 923 says:
YAHWEH—The vocalization of the four consonants of the Israylite name for the Creator, which scholars believe to approximate the original pronunciation.
The Wycliffe Bible Encyclopedia, page 690 tells us:
The Name par excellence for the Creator of Israyl is Yahweh, found 6,823 times in the OT. Through Israyl’s deliverance from bondage in Egypt, adoption as a nation, and guidance to the Promised Land, the Redeemer-Creator is especially known by THIS NAME. (Emphasis ours).
James Moffatt, in his translation, The Bible: A New Translation, 1935, Harper and Brothers, informs us in his introduction:
Strictly speaking this ought to be rendered Yahweh which is familiar to modern readers in the erroneous form of Jehovah. Were this version intended for students of the original, there would be no hesitation whatever in printing Yahweh.
Although Moffatt substitutes the title, The Eternal in the place of the Name of Yahweh, he fully admits a distinct loss of meaning in this.
The Encyclopedia Judaica, Volume 7, page 680 states emphatically:
The true pronunciation of the Name YHWH was never lost. Several early Greek writers of the Christian Church testify that the Name was pronounced Yahweh.
The Hebrew-Aramaic-English Dictionary, by Marcus Jastrow, Volume 1, page 576, proves that the abbreviation in the Targum Onkelos is that of Yahweh’s Name
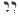

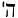
The book The Meaning of the Qumran Scrolls for the Bible page 164 tells us that in these original writings the Name Yahweh stood alone.
Actually this practice was much earlier, for one of the frequent discrepancies between the Massoretic text and the presumed Hebrew Vorlage of the Septuagint is whether to read in a given passage Yahweh alone, or Yahweh Adonai. This inconsistency was occasioned by the fact that originally Yahweh did stand alone, but that Adonai tended to be introduced alongside the Tetragrammaton by way of making explicit the surrogate. This was not understood by the Massoretes, however, who felt compelled to vocalize both words. Neither was it understood by the scribes of the Qumran Scrolls, nor even by still earlier translators of the LXX. That Yahweh originally stood alone in most passages is supported by the fact that, in Hebrew poetry, the double designation of the Deity usually adds excessive length to the poetic stich.
So not only do we have proof that the Name Yahweh was written in the original Holy Scriptures, we have proof that it was spoken by all of Yahweh’s people as well.
Yahweh’s Name is written yod-heh-waw-heh 
It thus becomes possible to determine with a fair degree of certainty the historical pronunciation of the tetragrammaton, the results agreeing with the statement of Ex. iii. 14, in which YHWH terms Himself 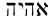

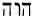
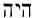
The personal Name of the Father of Israyl is written in the Hebrew Scriptures with the four consonants YHWH, and is referred to as the Tetragrammaton. At least until the destruction of the First Temple 586 B.C.E., Yahweh’s Name was pronounced regularly with its proper vowels, as is clear from the Lachish Letters, written shortly before that day. However, at least by the third century before our Messiah was born, the pronunciation of the Name Yahweh was avoided, and Adonai, the Lord, was substituted for it.
The Century Bible, Volume 1, pages 90-91 tells us:
Some time after the return from the Captivity, and before the beginning of the Christian Era, the Yahdaim (Jews) came to believe that the Holy Name YAHWEH was too sacred to be uttered on ordinary occasions. It was said to be pronounced by the High Priest on the Day of Atonement. At other times, when any one read or quoted aloud from what is called the Old Testament, the word Adonay, Lord, was usually substituted for Yahweh, and similarly the LXX (Septuagint Version) has Kurios, the Vulgate dominus, and the E.V. Lord, where the Hebrew has Yahweh. Hebrew was originally written without vowels, but when the vowel points were added, the vowels of Adonay or Elohim were written with Yahweh, as a direction that these words were to be read instead of the word whose consonants were Yahweh; thus we find the combinations YeHoWah and YeHoWiH. At the Reformation, the former being the more usual, was sometimes used as the Name of the (Mighty One) Of Israyl, and owing to ignorance of its history was misread as Jehovah, a form which has established itself in English, but does not give the pronunciation of the Holy Name it represents.

NEW YORK (AP)- Talk about holding on to a receipt.
A recently discovered piece of pottery recording a donation to the “House of Yahweh” may contain the oldest mention outside the Bible of King Solomon’s Temple.
The 3-1/2 by 4-inch artifact is nearly 3,000 years old, dating to a time when kings sent messenges inscribed on pottery. – 11/3/97
(AP Photo)
The Hiding Of Yahweh’s Name
In the Hebrew manuscripts, the religious scholars conclude there are three major texts of Scripture; the oldest and the original being the Yahwistic works, which use the Name of Yahweh exclusively. These works are referred to as the J writings because they contain only the Name of Yahweh without the pagan titles of El, Elohim or Adonai. In these first manuscripts, everyone knew instantly the Name of the Creator of all things, because the minds of those who read it were not confused by reading titles of pagan Gods (Elohim).
The next text of the Scriptures, coming about 100 years later, incorporated the use of pagan titles, which were adopted from the Canaanites after the children of Israyl entered the promised land, even though Yahweh had strictly warned them to stay away from the Godworship of the people they would come in contact with (Deuteronomy 7:1-5). In direct violation of Yahweh’s commandment not to worship hinder Gods (Elohim) only 100 years later the Holy Scriptures became polluted with the pagan titles of Elohim, Adonai, God and Lord.
The pagan word God comes from the word El (singular—God) or Elohim (plural—Gods).
From The Interpreter’s Dictionary of the Bible, Volume 1, page 817, we find the information that El or Elohim simply means demon.
A. In The OT. 1. Daimonism. a. Daimon. The Hebrew equivalent of “demon” (daimon) in the original sense is simply 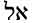
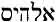
The words El-Elohim, like the words Baal-Adonai came from the Canaanite vocabulary and worship. These Canaanite words were accepted into the Hebrew language many years after the Yahwist writings of the Holy Scriptures.
The Encyclopedia Judaica, Volume 7, page 674 tells us:
Most of these terms were employed also by the Canaanites to designate their pagan gods. This is not surprising; since on settling in the Promised Land the Patriarchs and early Israelites made “the language of Canaan” their own (Is. 19:18), the Hebrew language would naturally use the Canaanite vocabulary for terms designating their own Deity.
These names of the Canaanites’ Gods (Elohim) were accepted before and during the time of Yeremyah the prophet began his prophesying.
Yeremyah 23:25-27—
25 I have heard what the prophets say, who prophesy lies in My Name, saying; I have dreamed! I have dreamed!
26 How long will this be in the heart of the prophets who prophesy lies? Yes, they are prophets of the deceit of their own minds;
27 Who devise; plan and scheme, tto cause My people to forget My Name through their dreams, which they tell every man to his neighbor, just as their fathers have forgotten My Name for Baal; Lord.
The word Baal simply means Lord, as is shown in Unger’s Bible Dictionary, page 665.
Lord (Hebrew Adon), an early word denoting ownership; hence, absolute control. It is not properly a (righteous) title…master; of kings, as the lords of their subjects. (4.) Lord. Master, (Greek Kurios) Supreme...
(5.) Baal (Master) (As noted above, it means Lord)—applied only to heathen deities (gods), or to man as husband, etc …
The Jews out of a superstitious reverence for the Name of Yahweh, always, in reading, pronounced Adonai where Yahweh is written.
On page 413 of Unger’s Bible Dictionary, we find:
Baal—common Canaanite word for master, lord, was one of the chief male deities of the Canaanite Pantheon, now well known from the religious epic literature discovered at Ras Shamra (an Ugarit of the Amarna Letters), from 1921-1937.
Smith’s Bible Dictionary on pages 195-196 states:
The substitution of the word Lord is most (sad); for, while it in no way represents the meaning of the Sacred Name, the mind has constantly to guard against a confusion with its lower uses, and, above all, the direct personal hearing of the Name on the revelation of Yahweh…is injuriously out of sight.
At the time, the use of these pagan terms was accepted, and used by the copyists to replace Yahweh’s Name, or to identify Him in their writings. However, these pagan words cannot identify Yahweh our Creator, because they are titles of Satan and her angels.
Unger’s Bible Dictionary page 412 states that the word El is a Canaanite word meaning God or devil.
The Interpreter’s Dictionary of the Bible, Volume 1, page 817, under Demonology, says the word Elohim (plural form of El) means demons or Gods.
Scholars and historians find it quite remarkable that the people of Yahweh ever accepted appellations such as Adonai or Elohim in place of the Name Yahweh. Harper’s Bible Dictionary by Paul Achtemeier, page 253 states:
The accomodation of El worship by Yahwism was a remarkable occurrence for Israel was as a rule hostile to the cults of Canaaite gods and goddesses.
The Encyclopedia Judaica, Volume 7 page 680, tells us a very important fact about Yahweh’s Name.
YHWH. The personal name… written in the Hebrew Bible with the four consonants YHWH and is referred to as the “Tetragrammaton.” At least until the destruction of the First Temple in 586 B.C.E. this name was regularly pronounced with its proper vowels, as is clear from the Lachish Letters, written shortly before that date. But at least by the third century B.C.E. the pronunciation of the name YHWH was avoided and Adonai,”the Lord,”was substituted for it.
Notice what they have written concerning the Name Yahweh from The Torah: A Modern Commentary, by Gunther Plaut, page 31 and page 426.






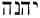

Overwhelming scholarly opinion holds that 

), which may represent the original form from which Yahweh was expanded or may, contrariwise, be a contraction of the longer ascription. Yahweh occurs sometimes alone (as in 15:2, 17:16), but more likely in conjunction with proper names like Elijah (Eliyah in Hebrew) and in the doxology, HalleluYahweh.
The Name Yahweh means self-existent, which this source shows. But it also means perfect righteousness, which is contrary to the meaning of the word God, which means a mixture of righteousness and evil. Notice the following Scriptures, which shows the character of Yahweh:
Exodus 33:18-19—
18 Then Mosheh said; Show me now Your glory.
19 And Yahweh said: I will make all My righteousness pass in front of you; and I will proclaim My Name, YAHWEH , in your presence. I will have mercy on whom I will have mercy, and I will have compassion on whom I will have compassion.
Exodus 34:5-7—
5 Then Yahweh descended in the cloud, and stood with him there, and proclaimed the Name of YAHWEH.
6 Yahweh passed in front of him, and proclaimed: YAHWEH, YAHWEH Almighty, merciful and compassionate, longsuffering, and abounding in righteousness and truth.
7 Keeping mercy for thousands, forgiving iniquity, and transgression, and sin; but by no means leaving unpunished those who are guilty; Who visits the sin of the fathers upon the children and the children’s children, to the third and fourth generation.
They have substituted (among many other names and titles) Baal, the Babylonians God (el) and Adonay, the Canaanite God (El) of the Phoencians for the holy Name of our Creator Yahweh. The substitution of Yahweh’s Name with the names of pagan Gods (Elohim) has brought immeasurable harm. Such names as Lord, God, Jesus and Christ in no way represent the meaning of the name revealed by Yahweh our Heavenly Father to Mosheh, and to the ancient Hebrews. By employing these names, the people unknowingly turn the worship of Yahweh into that of God (elohim) and actually ascribe the loving and merciful characteristics of the Father of Israyl, to the pagan Gods (Elohim).
The New International Version Interlinear Hebrew-English Old Testament, elects to use Yahweh’s Name where it is written in the Hebrew text. In Volume 1, page 26 of the Introduction is found this statement:
Yahweh, the personal Name of (the Creator) is always translated Yahweh, against the practice in the NIV in rendering it as Lord. On the one hand, this prevents confusion of the Name with the title (Adonai) my Lord, for the idea of lord is not an integral element of the Name. On the other hand, it may be the use of Yahweh in this work will encourage the reader to use the personal Name of (Yahweh) in prayer and praise, as is intended by the most common imperative in the Scriptures: (HalleluYahweh!) Psalm 104:35: Praise Yahweh!
Importance Placed On Yahweh’s Name!
The Holy Name of our Father and Creator, Yahweh is the one and only Name by which the Creator is known throughout the Holy Scriptures.
Psalm 23:6—
Surely righteousness and mercy will follow us all the days of our lives; an we will dwell in the House of Yahwehforever!
Psalm 9:10—
They that know your Name will put their trust in You! Those who seek You, You will not forsake!
Psalm 83:18—
Let men know that You, whose Name alone is Yahweh, are the Supreme Head over all the earth!
Isayah 43:3—
For i am Yhweh your Father, the Holy One of Israyl, your Savior…
Following is a list of only a few of the Scriptures which show the glorification of Yahweh’s Name in His Book:
Psalm 68:4, Exodus 17:8-15, Exodus 15:26, Judges 6:24, Genesis 22:13-14, Acts 2:21, Yeremyah 23:6, Proverbs 30:4, Isayah 42:8, Hosheyah 2:17, Hebrews 2:12, Psalm 22:22, I Kings 18:21, Yahchanan 12:13, Yahchanan 14:13-14, Acts 4:12.
Throughout the Holy Scriptures, you can read of the importance placed on the Name of Yahweh. Knowing and using our Creator’s Name in worship and study has been important for each generation, for Yahweh is the only Being Who can give life.
I Timothy 6:16—
WHO ALONE HAS IMMORTALITY, dwelling in the light which no man can approach unto; Whom no man has seen, nor can see; to whom belongs honor and power everlasting. HalleluYahweh! Praise Yahweh!
This Scripture alone shows the great importance that is attached to knowing our Heavenly Father’s Name. But as this age grows closer to an end and all hope of life slowly vanishes, it becomes extremely important for people to know our Creator’s Name. It is only those who call with the Name of Yahweh who will be delivered at this end time.
Yahyl 2:31-32—
31 The sun will be turned into darkness, and the moon into blood, before the great and the terrible day of Yahweh comes.
32 And whoever will call with the Name of Yahweh will be delivered; for in Mount Zion in Yerusalem there will be deliverance, as Yahweh has said, among the remnant who has escaped of those whom Yahweh calls.
How will Yahweh, our Creator, hear us if we continue to call upon Him with the titles of pagan Gods (Elohim)?
There Is No Denying The Greatness
Of Yahweh’s Name
There is simply no denying the importance of the Name of Yahweh, to Yahweh’s people. The simple fact is that if we are not, or will not become, willing to invoke and be called with Yahweh’s Name, we have no hope at all for any salvation. The holy men of old, we supposedly look to as our teachers and examples, called with the Name of Yahweh. Why then are we still so stubborn? We must obey Yahweh’s every word and heed the examples of the holy people of old, to call with Yahweh’s Name.
A true “devout” Israyli will not mention the names of pagan gods, but will only call on Yahweh. Notice what is written in The Jewish Encyclopedia, Volume 9, page 160.
The devout Israelite will not take the name of a false god upon his lips (Ex. xxiii. 13; Josh. xxiii. 7; Hosea ii. 16-17; Ps. xvi. 4). To make mention of YHWH’s name is to asse. confidence in His strength and present and efficient aid. The name excites emotions of love, joy, and praise. (Ps. v. 11; vii. 17; ix. 2; xx. 1, 7). That name is, therefore, especially connected with the altar or sanctuary, the place where Yahweh records His name (Ex. xx. 24), or “the place where Yahweh shall choose out of all your tribes to put His name there.” (Deut. xii. 5; comp. I Kings viii. 16, 29; ix.. 3; Jer. vii. 12). The Temple is “the place of the name of Yahweh of hosts, the mount Zion.” (Isa. xviii. 7).
The Encyclopedia Britannica, Volume 23, page 867, also tells us about the meaning of Yahweh’s Name to Israylites.
This presence and power of Yahweh is stressed in the frequent biblical phrase “Yahweh Sabaoth,” “Yahweh of hosts,” those hosts both earthly and heavenly which Yahweh uses to establish his sovereignty over Israel, and through Israel over the whole world. The name Yahweh was thus for the faithful Israelite a never-failing source of confidence, power and joy.
Yahweh is, most certainly, our Father and the source of our salvation. He will give salvation to those who follow Him completely, refusing to bow to or serve God (any Gods) at all. There is overwhelming proof that the words El and Elohim were the very words the pagan Canaanites used for worshipping their own Gods. It is obvious from the study of the etymology of the Hebrew language, that the Children of Israyl made the language of Canaan their own because of the snares of the Canaanites and their own disobedience to Yahweh. As we have seen, the word El has been translated as God in many Scriptures, but it is of vital importance to know that this word has also been translated power in three different Scriptures.
Genesis 31:29—
It is in my power to do you harm, but Yahweh, the Father of your father, spoke to me last night, saying: Be careful that you speak to Yaaqob neither blessings nor curses.
Proverbs 3:27—
Do not refuse help to one who has need of it when it is in the power of your hand to give it.
Micahyah 2:1—
Woe to those who devise iniquity, who plot evil upon their beds! When the morning dawns they carry out their plans, because it is in their power to do so.
In each of these three verses, the word El has been translated power, which is power of man, not Yahweh. El, word #410 in the Hebrew Dictionary of Strong’s Exhaustive Concordance comes from another Hebrew word #352, which is the same as #193. The root of these words means powerful, mighty or strength.
The Encyclopedia Judaica, Volume 7, page 674, gives us the following information.
‘El. The oldest Semitic term for God is `el (corresponding to Akkadian ilu (m), Canaanite ‘el or ‘il, and Arabic ‘el as an element in personal names). The etymology of the word is obscure. It is commonly thought that the term derived from a root `yl or `wl meaning “to be powerful.”
Strong’s Exhaustive Concordance Hebrew Dictionary confirms this statement. El, comes from word #352, ayil, which means:
410. 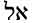
352. 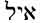
Ayil is from the same unused root as uwl, ool, meaning:
193. 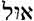
We see that King David, a man after Yahweh’s own heart, acknowledged that Yahweh was his strength, but certainly not a God.
Psalm 22:19—
But You, O Yahweh, be not far from Me! O My Strength, make haste to help Me!
Strength in this verse is word #360 in the Hebrew Dictionary of Strong’s Exhaustive Concordance, and means power, by implication, protection, strength.
360. 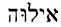
Eyaluwth comes from the word eyal, which comes from ayil, which comes from the same unused root uwl, which means:
353. 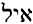
Psalm 22:1, “My Yl” and Psalm 22:19, “My Strength,” have the same root word, and the same meaning: My Strength.
We have already read that El and Elohim were Canaanite words relating to Canaanite gods that Yahweh condemns. Notice the definitions of El and Elohim.
410. 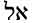
430. 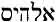
The direct work of the elohist writer has been to place the names of the Gods of Canaan, into the Holy Scriptures. The Canaanites took the idols of strength and power, contained in the primitive roots yl and wl, and made Gods out of these concepts. Israylites have fallen for this deception and now worship Elohim instead of Yahweh, Who is truly the only source of power (Isayah 44:6,8).
Gesenius Hebrew-Chaldee Lexicon, page 45, shows us more about the word EL.
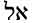
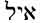
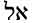
Notice the note by the author of this Lexicon which says:
Note. Following most etymologists, I have above derived 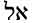
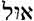
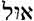
From man’s own writings, we see this 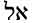
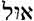
Gesenius Hebrew-Chaldee Lexicon, page 20, also gives us this information on ayil (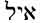
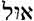
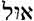
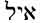
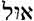
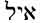
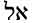
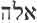
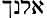
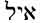
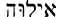
According to Gesenius Hebrew-Chaldee Lexicon To The Old Testament, page 695, this word El originally came from the root words wl and yl. Man’s own writings say these words mean strength, power, strong. These writings also say that the words El-God and elohim-god, were the work of a later and deceived writer.
Yahweh is the only source of power we can turn to in time of need, and there has never been a time we needed Yahweh more than this present age with the dangers we are facing.
Yahshua 23:5-8—
5 Yahweh your Father Himself will drive them out of your way. He will push them out from in front of you, and you will take possession of their land, just as Yahweh your Father has promised you.
6 Therefore, be very strong to carefully obey and do all that is written in the Book of the Law given through Mosheh, without turning aside either to the right or to the left;
7 By not mingling with these nations that are left with you: by not pronouncing the names of their gods (elohim), nor causing anyone to administer a vow in their names. You must not serve them, and you must not bow down to them.
8 You are to hold fast to Yahweh your Father, just as you have until now.
Yahweh has told us in no uncertain terms not to even say the names of their Gods to worship them. How much plainer could this be? Yahweh has also shown us the words El and Elohim, God and Lord are the names of the very Canaanite Gods He told us not to mention.
At the time Yahshua was leading the Children of Israyl, they had not worshipped Gods, they had not bowed themselves to, nor had they served the Lord—they had not forsaken Yahweh. Yahweh was their (and our) strength, head and Father. Yahweh was not then, nor has He ever been, a mere God. That is why we must return the prefixes and suffixes El-God to Yl-strength-Father, to give honor to Yahweh by not making mention of the names of their Gods out of our mouths. Yahweh only allows those who submit to Him to carry His Name.
Isayah 52:6—
Therefore My people will know My Name; Therefore they will know in that day that I am He Who speaks. Behold, it is I!

Click to DOWNLOAD Just visit one of our publication pages to download our free monthly magazine, free monthly newsletter, free booklet page or contact us with any questions or comments.
The House of Yahweh – P.O. Box 2498 – Abilene, Texas 79604
(c)2004 A House of Yahweh Publication (R)TM

 ): High priest. He is identical either with Simeon I. (310-291 or 300-271 b.c.), son of Onias I., and grandson of Jaddua, or with Simeon II. (219-199 b.c.), son of Onias II… After Simeon’s death men ceased to utter the tetragrammaton aloud (Yoma 30b; Tosef Sotah. xiii.).
): High priest. He is identical either with Simeon I. (310-291 or 300-271 b.c.), son of Onias I., and grandson of Jaddua, or with Simeon II. (219-199 b.c.), son of Onias II… After Simeon’s death men ceased to utter the tetragrammaton aloud (Yoma 30b; Tosef Sotah. xiii.). 




